6 Analyse de variance

Mise en place : Télécharger le dossier exo6 et décompressez le sur votre ordinateur. Puis ouvrez le projet R exo6.Rproj dans Rstudio.

6.1 Préparation des données

6.1.1 Chargement du fichier

On charge un fichier statistique appelé tips.csv où les séparateurs sont des points-virgules et les décimales des points.

don<-read.table(file = "resources/data/tips/tips.csv",
                sep = ";",
                header = T)
head(don)

  IDEN TOTBILL  TIP SEX SMOKER DAY TIME SIZE
1 R001   16.99 1.01   1      0   6    1    2
2 R002   10.34 1.66   0      0   6    1    3
3 R003   21.01 3.50   0      0   6    1    3
4 R004   23.68 3.31   0      0   6    1    2
5 R005   24.59 3.61   1      0   6    1    4
6 R006   25.29 4.71   0      0   6    1    4

6.1.2 Contenu du fichier

Ce dossier contient les pourboires (tips en anglais, d’où le nom du fichier) d’un serveur dans un restaurant américain aux débuts des années 1990. Le restaurant était dans un centre commercial. Il y avait une zone fumeurs et une zone non fumeurs.Les données indiquent le prix du repas, le pourboire, le sexe de la personne qui a payé et donné le pourboire, si c’était dans la zone fumeurs ou non, le jour où le repas a été pris, si c’était en journée ou en soirée et enfin, le nombre de convives.

Sources : Ces données sont disponibles dans le package R nommé rggobi et sont décrites dans l’ouvrage de Cook et Swayne intitulé Interactive and Dynamic Graphics for Data Analysis. Elles font partie des données d’exemple du livre de Bryant et Smith dont la première édition est parue en 1995 dont le titre est Practical Data Analysis: Case Studies in Business Statistics.

6.1.3 Dictionaire des variables

IDEN : identifiant du repas
TOTBILL : prix du repas (en dollars des années 1990)
TIP : pourboire (en dollars des années 1990)
SEX : sexe de la personne qui a payé (0 = Homme, 1 = Femme)
SMOKER : la personne qui a payé est non-fumeur (O) ou fumeur (1)
DAY : jour de la semaine (1 = dimanche, 2 = lundi, 3 = mardi, …)
TIME : repas pris en journée (0) ou le soir (1)
SIZE : nombre de convives

6.1.4 Recodage des variables

Le type de plusieurs variables est incorrect. On transforme les codes numériques en facteur et on recode les niveaux en français :

don$IDEN<-as.character(don$IDEN)
don$SEX<-as.factor(don$SEX)
levels(don$SEX)<-c("Homme","Femme")
don$SMOKER<-as.factor(don$SMOKER)
levels(don$SMOKER)<-c("Non fumeur", "Fumeur")
don$DAY<-as.factor(don$DAY)
levels(don$DAY)<-c("Mercredi","Jeudi","Vendredi","Samedi")
don$TIME<-as.factor(don$TIME)
levels(don$TIME)<-c("Journée","Soirée")

6.1.5 Ajout d’une nouvelle variable

On crée la variable PCT qui est le rapport entre le pourboire (TIP) et le prix total (TOTBILL) du repas exprimé en pourcentage.

don$PCT<-100*don$TIP/don$TOTBILL

6.1.6 Résumé de l’ensemble du tableau

summary(don)

     IDEN              TOTBILL           TIP            SEX     
 Length:244         Min.   : 3.07   Min.   : 1.000   Homme:157  
 Class :character   1st Qu.:13.35   1st Qu.: 2.000   Femme: 87  
 Mode  :character   Median :17.80   Median : 2.900              
                    Mean   :19.79   Mean   : 2.998              
                    3rd Qu.:24.13   3rd Qu.: 3.562              
                    Max.   :50.81   Max.   :10.000              
        SMOKER          DAY          TIME          SIZE           PCT        
 Non fumeur:151   Mercredi:62   Journée: 68   Min.   :1.00   Min.   : 3.564  
 Fumeur    : 93   Jeudi   :19   Soirée :176   1st Qu.:2.00   1st Qu.:12.913  
                  Vendredi:87                 Median :2.00   Median :15.477  
                  Samedi  :76                 Mean   :2.57   Mean   :16.080  
                                              3rd Qu.:3.00   3rd Qu.:19.148  
                                              Max.   :6.00   Max.   :71.034

6.2 Rappels sur la régression

6.2.1 La distribution de PCT est-elle normale ?

hist(don$PCT, breaks = 10,col="lightyellow",probability = TRUE)
lines(density(don$PCT,bw=3),col="red",lwd=1)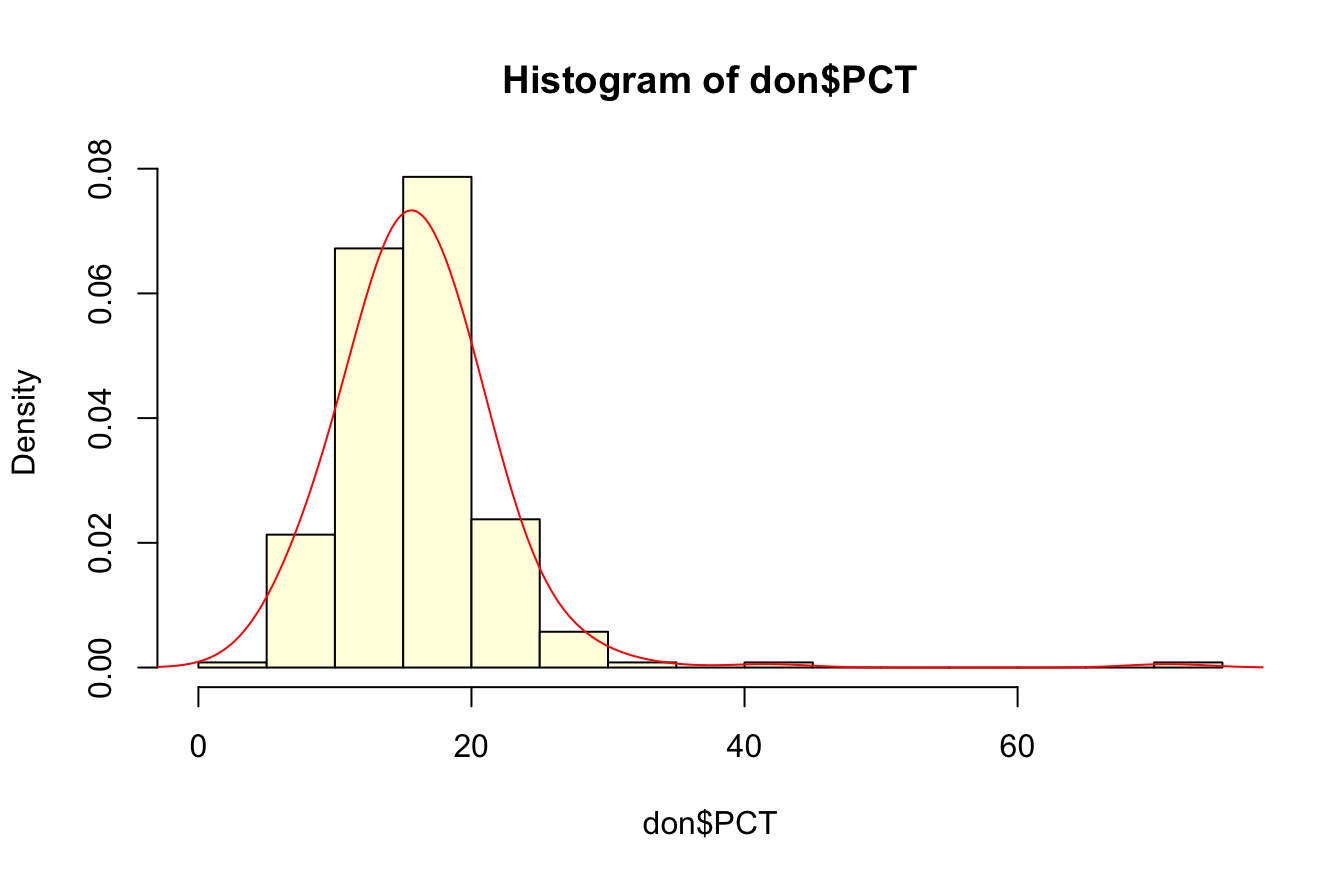

La distribution semble normale . Mais est-ce l’avis du test de Shapiro ?

shapiro.test(don$PCT)


    Shapiro-Wilk normality test

data:  don$PCT
W = 0.79943, p-value < 2.2e-16

Que nous apprend la boxplot ?

boxplot(don$PCT, col="lightyellow",horizontal = T)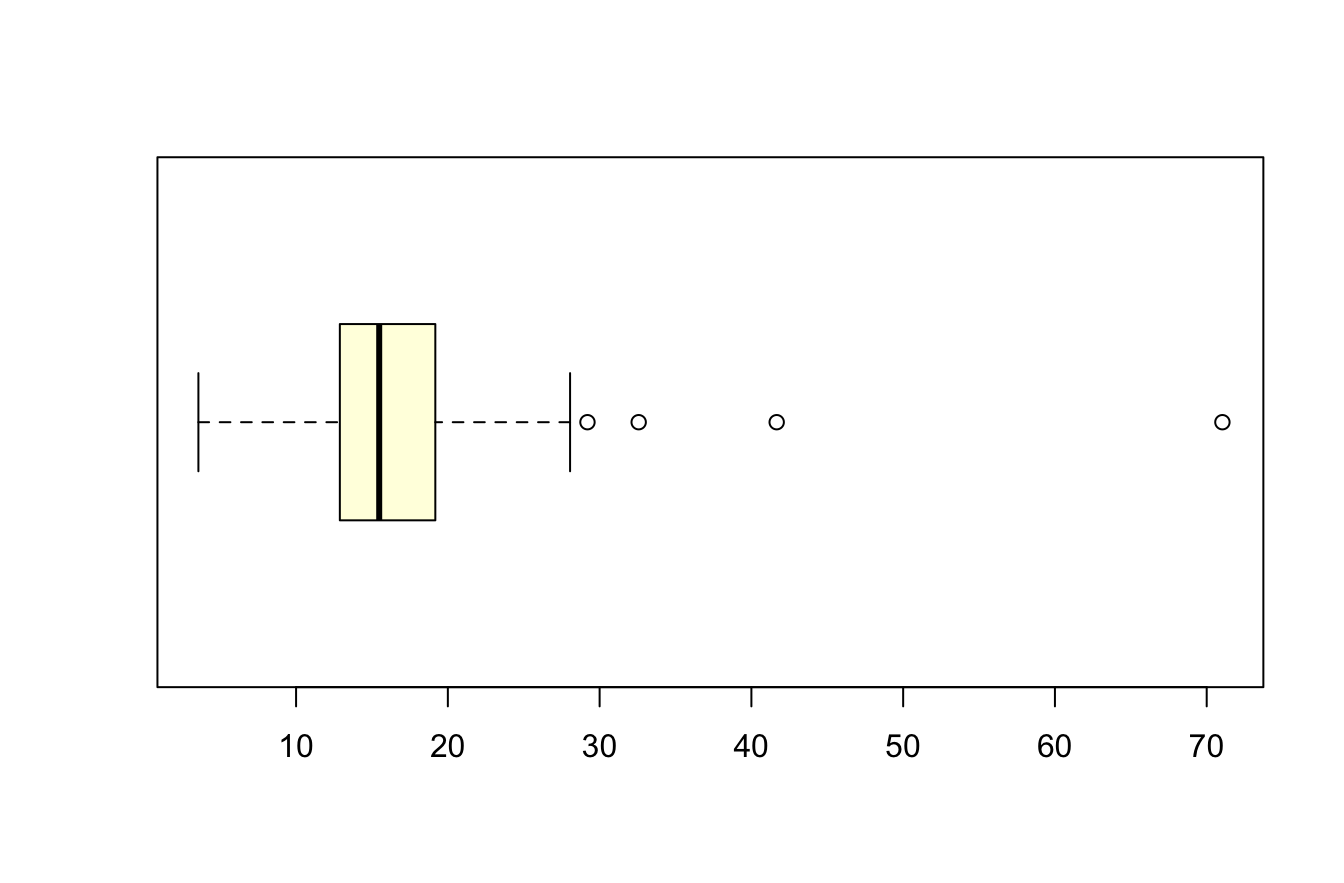

La distribution devient presque parfaitement gaussienne si on retire les 4 valeurs exceptionnelles !

don2<-don[don$PCT<30,]
shapiro.test(don2$PCT)


    Shapiro-Wilk normality test

data:  don2$PCT
W = 0.99435, p-value = 0.5066

hist(don2$PCT, breaks = 10,col="lightyellow",probability = TRUE)
lines(density(don2$PCT,bw=3),col="red",lwd=1)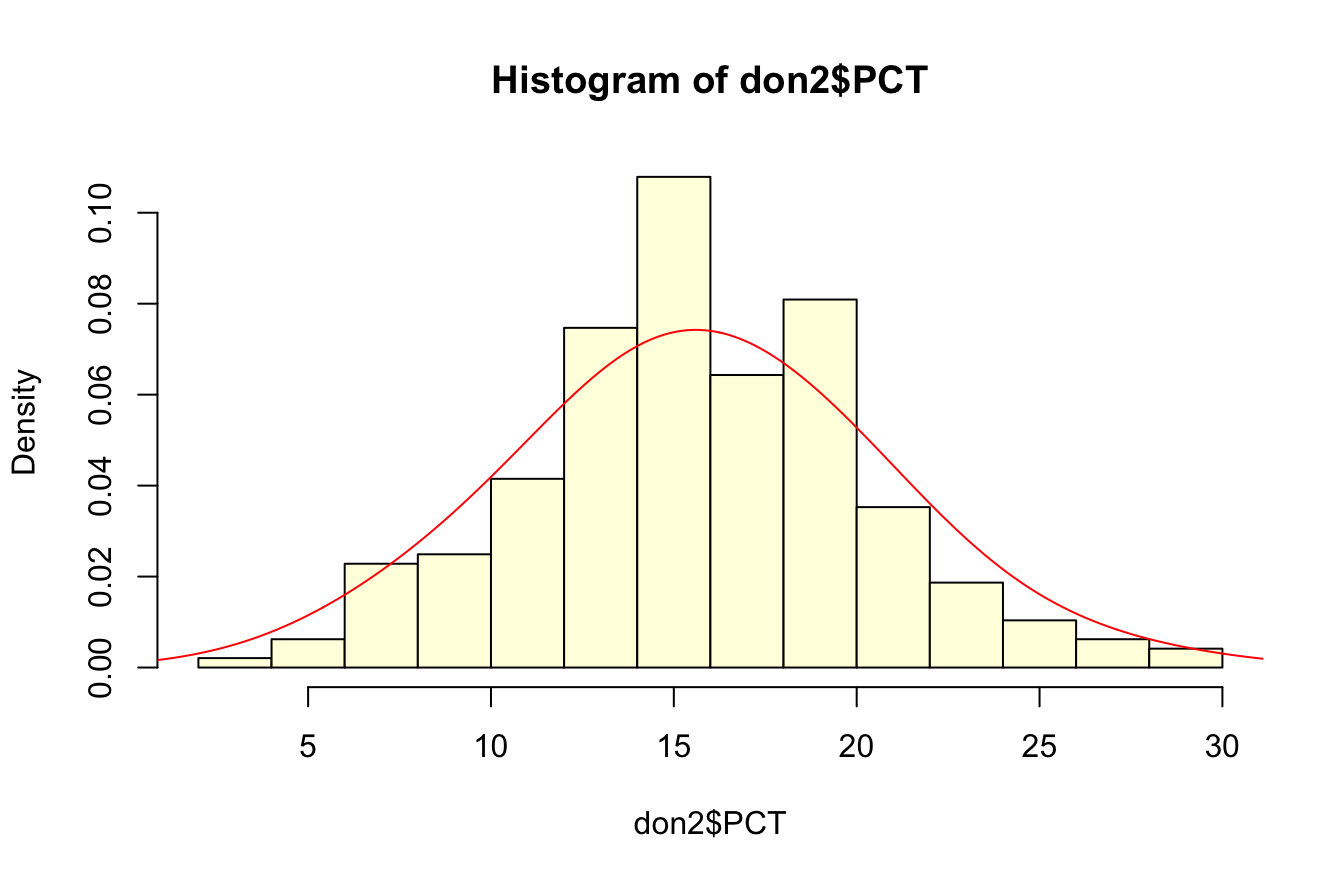

6.2.2 Y-a-t-il une relation entre le prix du repas et le pourboire ?

On fait le graphique …

plot(don2$TOTBILL,don2$TIP)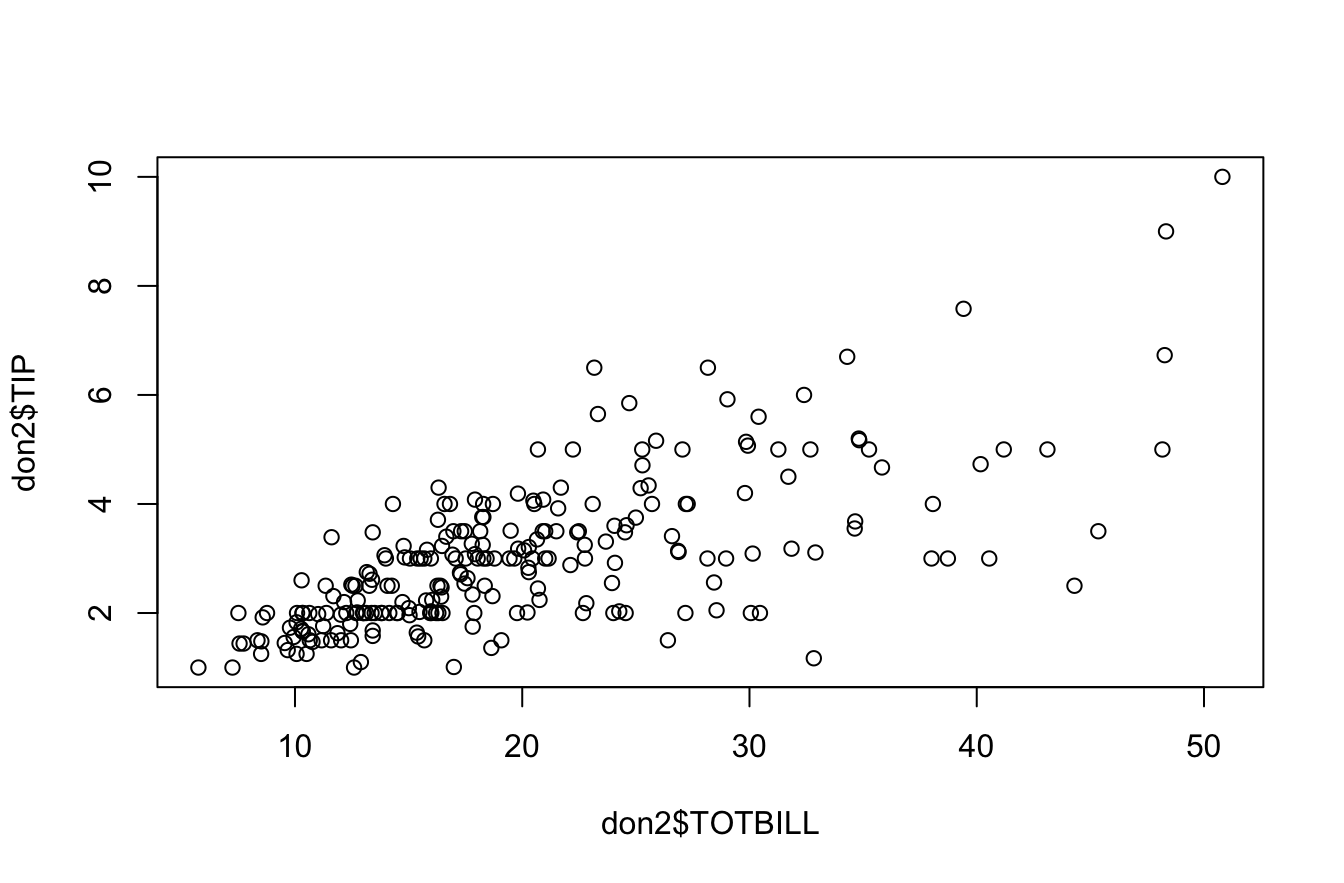

Puis on teste le coefficient de Pearson et celui de Sperman

cor.test(don2$TIP,don2$TOTBILL)


    Pearson's product-moment correlation

data:  don2$TIP and don2$TOTBILL
t = 14.906, df = 239, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.6223204 0.7543075
sample estimates:
      cor 
0.6941023

cor.test(don2$TIP,don2$TOTBILL, method="spearman")

Warning in cor.test.default(don2$TIP, don2$TOTBILL, method = "spearman"):
Cannot compute exact p-value with ties


    Spearman's rank correlation rho

data:  don2$TIP and don2$TOTBILL
S = 688482, p-value < 2.2e-16
alternative hypothesis: true rho is not equal to 0
sample estimates:
      rho 
0.7048791

6.2.3 Modèle de régression

On calcule le modèle de régression

mareg<-lm(don2$TIP~don2$TOTBILL)

plot(don2$TOTBILL,don2$TIP, xlab="Repas ($)",ylab = "Pourboire ($)",pch=19,cex=0.5)
abline(mareg,col="red",lwd=1)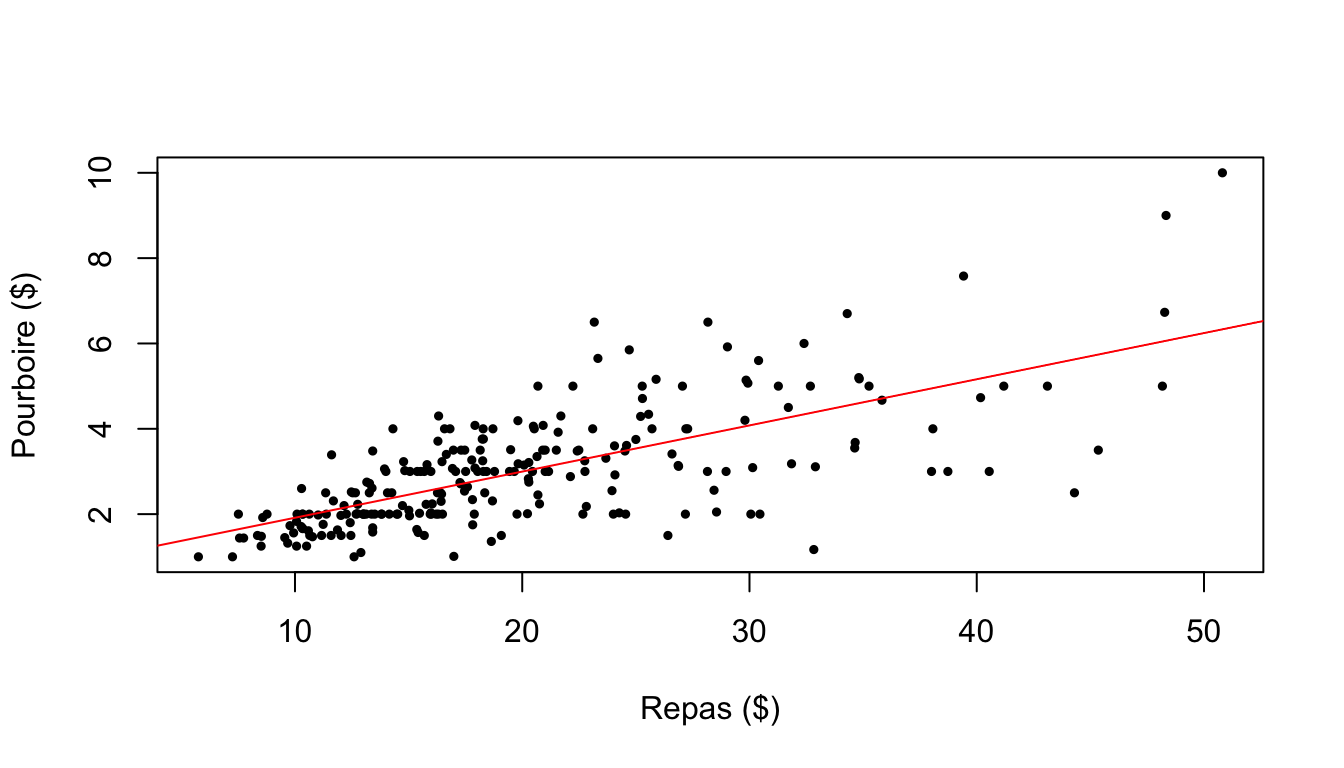

6.3 Test d’égalité des moyennes

6.3.1 Hypothèses

On considère une variable Y quantitative continue définie sur une population de réféence P et une variable X qualitative à deux modalités divisant P en deux sous population P1 et P2.

Soit par exemple la variable Y = PCT et la variable X = SEX. On peut se demander si les femmes sont plus généreuses que les hommes, les hommes sont plus généreux que les femmes, les hommes sont différents des femmes, etc…

Y<-don2$PCT
nomY <-"Pourboire relatif (%)"

X<-don2$SEX
nomX <- "Sexe du client"

#X<-don2$SMOKER
#nomX<- "Tabagisme"

#X<-don2$TIME
#nomX<- "Moment de la journée"

6.3.2 Visualisations

Le plus simple est d’utiliser boxplot() en version de base …

boxplot(Y~X)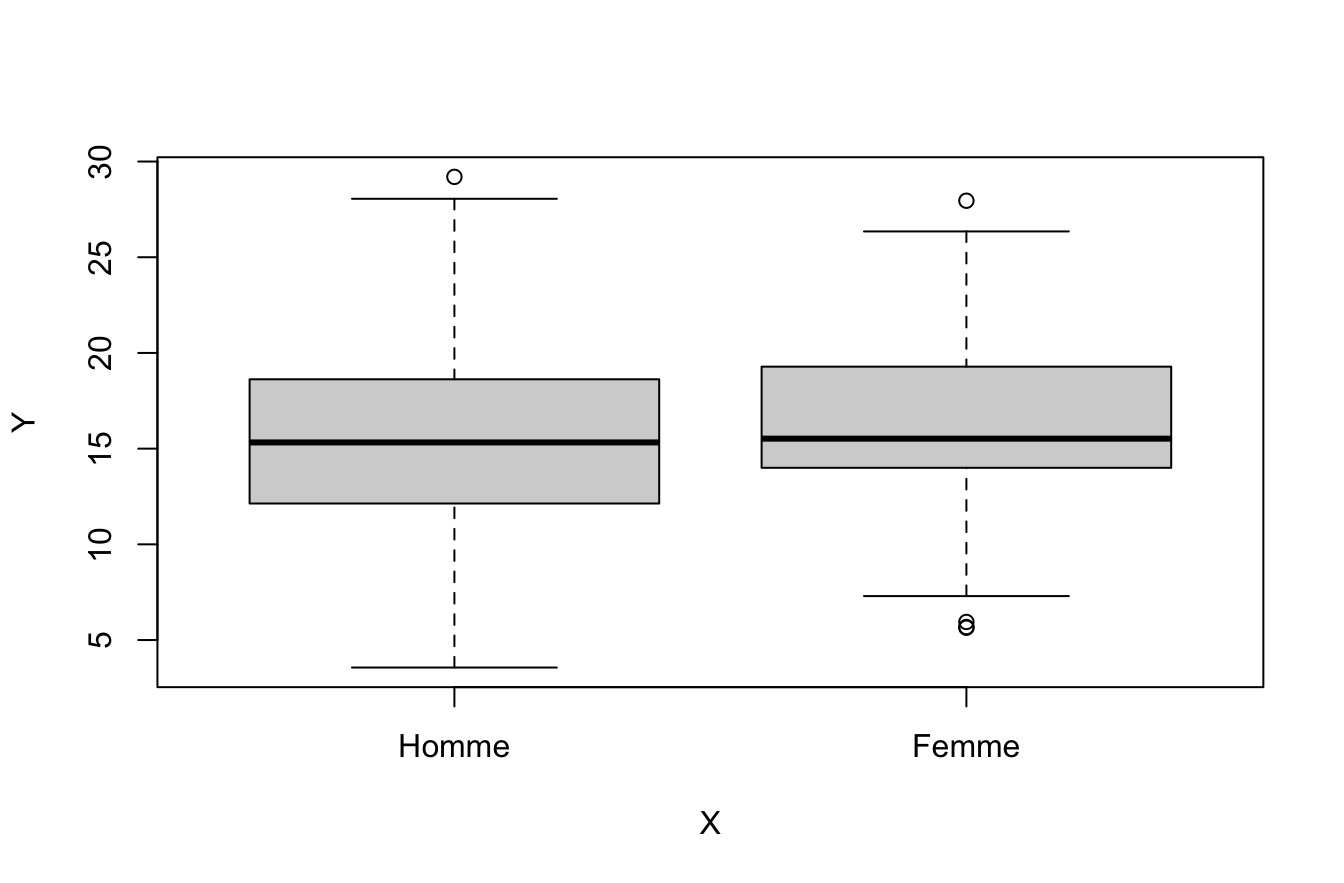

… ou améliorée

boxplot(Y~X,horizontal=T, xlab = nomY, ylab=nomX, col="gray80")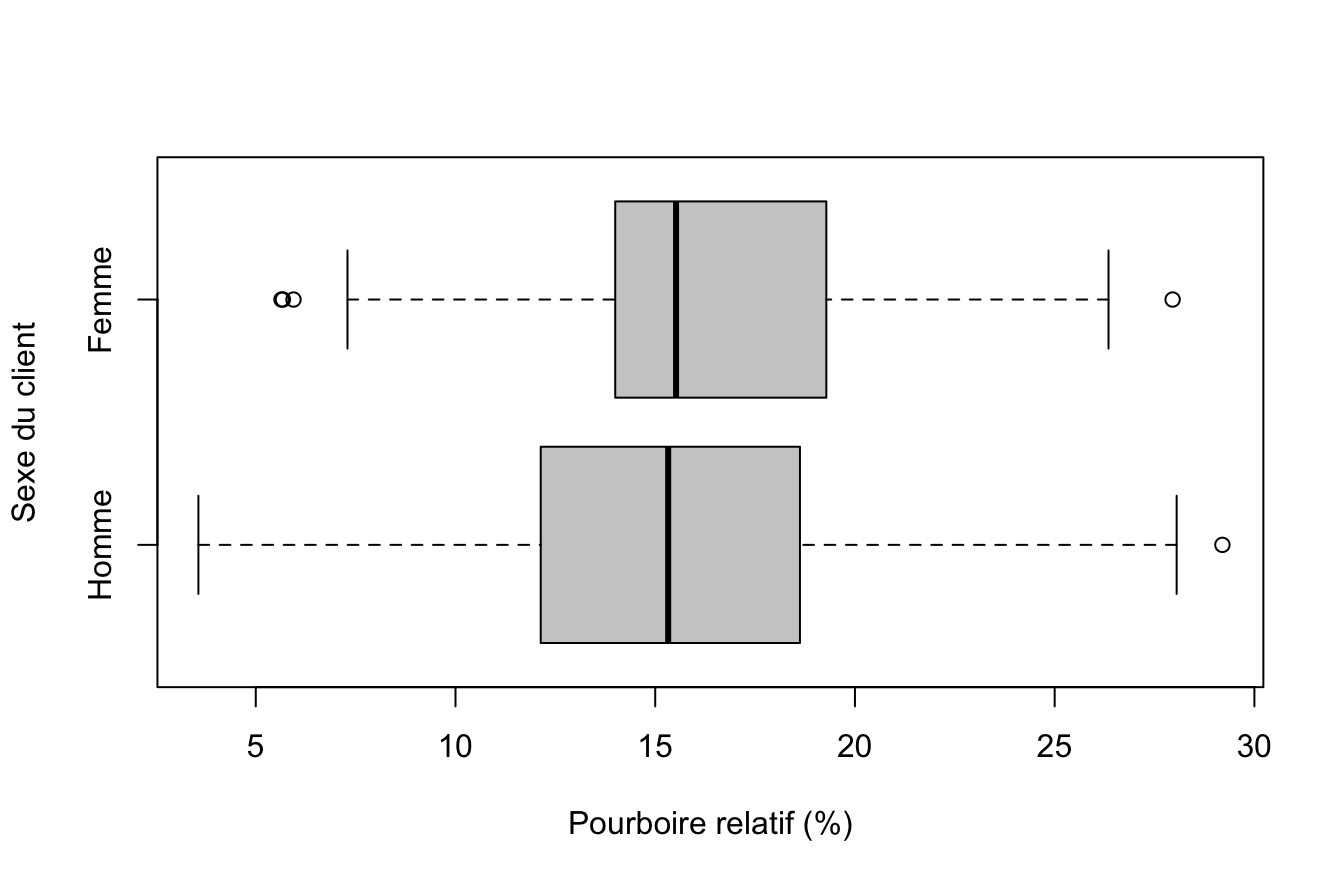

On peut aussi utiliser le package beanplot() en version simple …

library(beanplot)
beanplot(Y~X)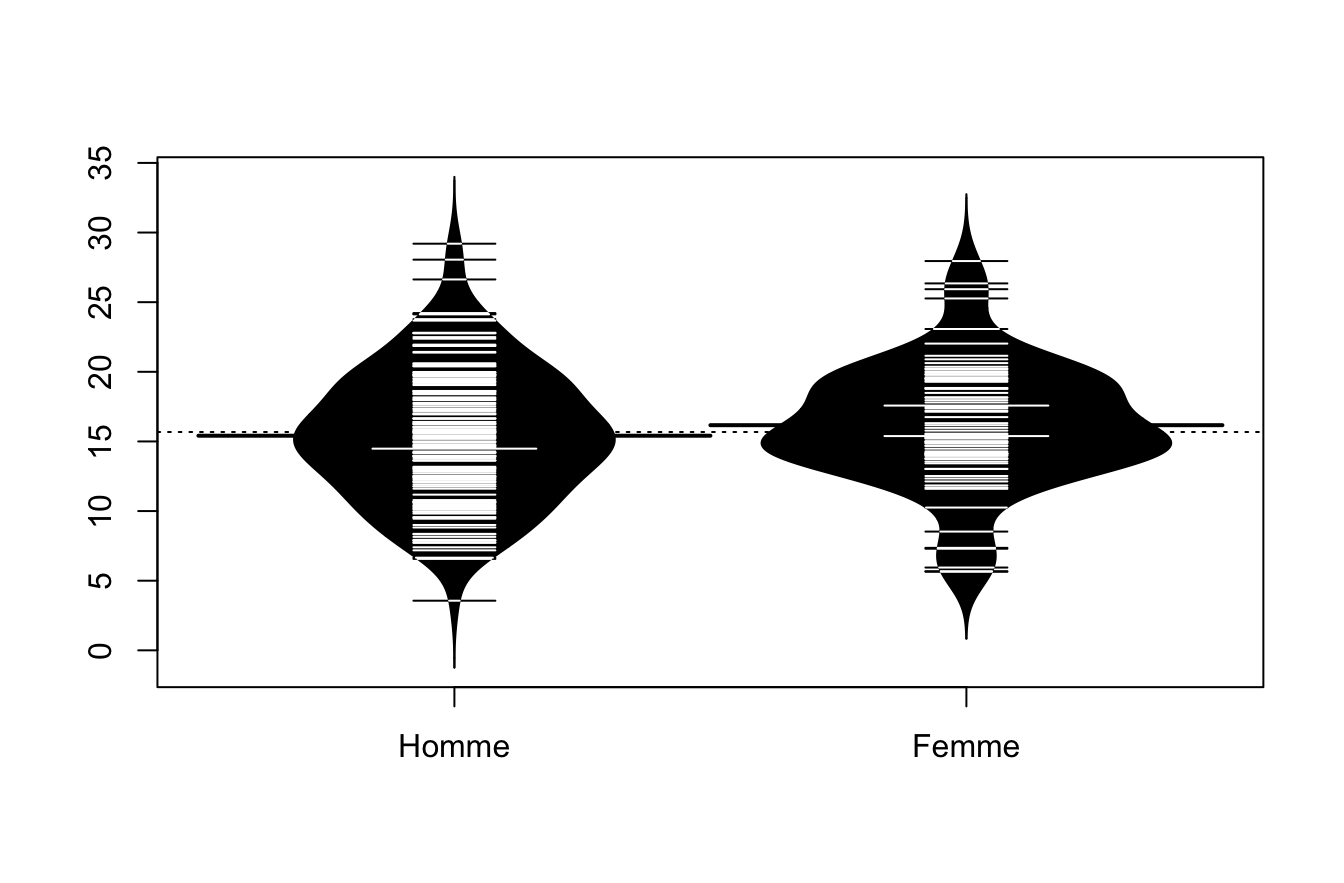

… ou améliorée :

library(beanplot)
beanplot(Y~X,horizontal=T, xlab = nomY, ylab=nomX,col = "gray80")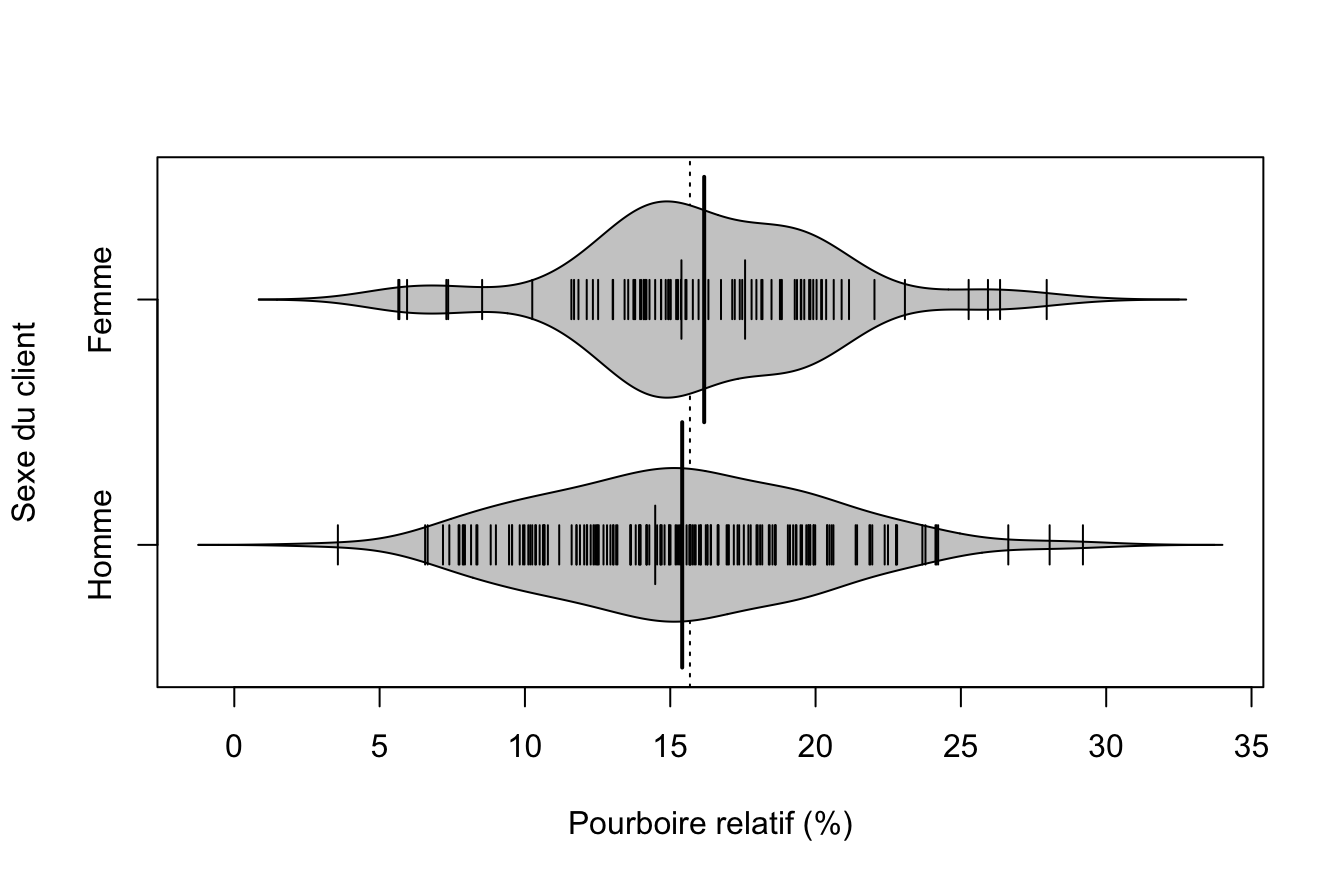

6.3.3 Paramètres principaux

On détermine la moyenne et l’écart-type de chaque échantillon avec la fonction tapply() couplée avec les fonctions mean(), sd() ou summary()

tapply(Y,X, mean)

   Homme    Femme 
15.41076 16.16741

tapply(Y,X,sd)

   Homme    Femme 
4.732686 4.329426

tapply(Y,X, summary)

$Homme
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  3.564  12.136  15.325  15.411  18.622  29.199 

$Femme
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  5.643  13.999  15.522  16.167  19.284  27.952

6.3.4 Test d’égalité des moyennes

Si la distribution est gaussienne on utilise le test de Student :

t.test(Y~X)


    Welch Two Sample t-test

data:  Y by X
t = -1.254, df = 186.21, p-value = 0.2114
alternative hypothesis: true difference in means between group Homme and group Femme is not equal to 0
95 percent confidence interval:
 -1.9470273  0.4337437
sample estimates:
mean in group Homme mean in group Femme 
           15.41076            16.16741

Si ce n’est pas le cas et s’il y a des valeurs exceptionnelles on préfèrera le test de Wilcoxon basé sur les rangs des valeurs (comme le coefficient de corrélation de Spearman)

wilcox.test(Y~X)


    Wilcoxon rank sum test with continuity correction

data:  Y by X
W = 5953, p-value = 0.1908
alternative hypothesis: true location shift is not equal to 0

Lorsque les deux tests divergent dans leur conclusions, il y a certainement un problème de violation de l’hypothèse gaussienne. Dans ce cas, il faut sans doute transformer Y ou retirer des valeurs exceptionnelles (Cf.cours sur la corrélation et la régression)

6.4 Analyse de variance

6.4.1 Hypothèses

On considère une variable Y quantitative continue définie sur une population de réféence P et une variable X qualitative à k modalités divisant P en k sous population P1…Pk.

Soit par exemple la variable Y = PCT et la variable X = DAY. On peut se demander si la générosité des pourboires varie en fonction des jours de la semaine (mercredi, jeudi, vendredi ou samedi). On fera toutefois attention au fait que l’échantillon n’est pas très équilibré

table(don2$DAY)


Mercredi    Jeudi Vendredi   Samedi 
      62       19       86       74

6.4.2 Calcul des paramètres principaux

On va calculer les paramètres principaux de chacune des quatre sous population à l’aide de la superfonction tapply() dont la syntaxe est la suivante

tapply(variable à analyser, variable de partition , function)

La fonction tapply() s’applique sur les tableaux (data.frame). Il y a des fonctions équvalentes pour les listes, les matrices, etc…

moy<-tapply(X = don2$PCT, INDEX = don2$DAY, FUN = mean)
moy

Mercredi    Jeudi Vendredi   Samedi 
16.12756 16.99130 15.11450 15.61781

ect<-tapply(don2$PCT, don2$DAY, sd)
ect

Mercredi    Jeudi Vendredi   Samedi 
3.865182 4.766531 4.803544 4.858665

100*ect/moy

Mercredi    Jeudi Vendredi   Samedi 
23.96631 28.05277 31.78104 31.10976

tapply(don2$PCT, don2$DAY, summary)

$Mercredi
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  7.296  13.821  15.385  16.128  19.269  26.631 

$Jeudi
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  10.36   13.37   15.56   16.99   19.66   26.35 

$Vendredi
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  3.564  12.373  15.099  15.114  18.767  29.199 

$Samedi
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  5.945  11.737  15.965  15.618  18.494  28.054

6.4.3 Visualisation

On utilise comme précédemment boxplot() :

boxplot(don2$PCT~don2$DAY, col="gray80")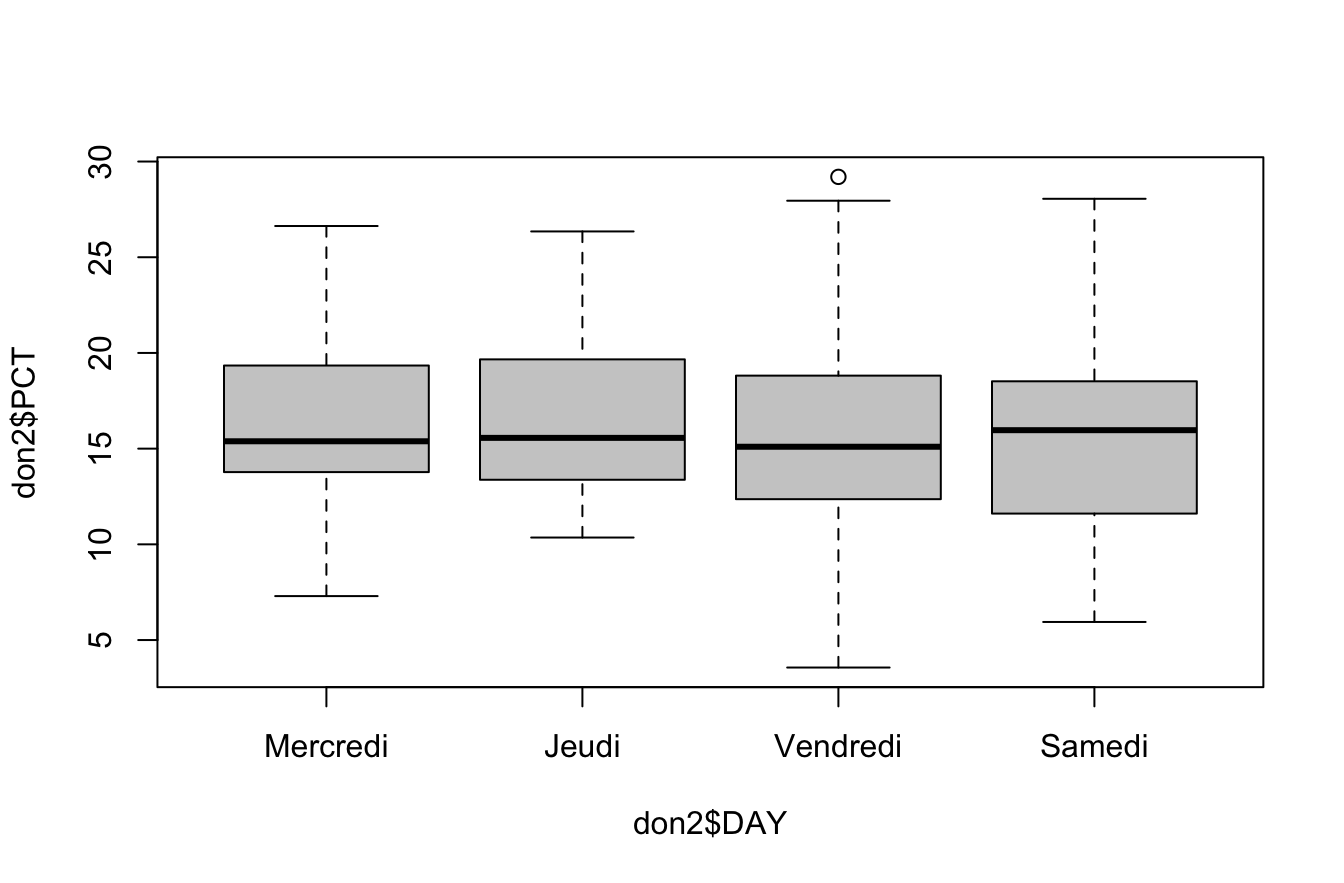

Ou bien beanplot() :

library(beanplot)
beanplot(don2$PCT~don2$DAY,col = "gray80")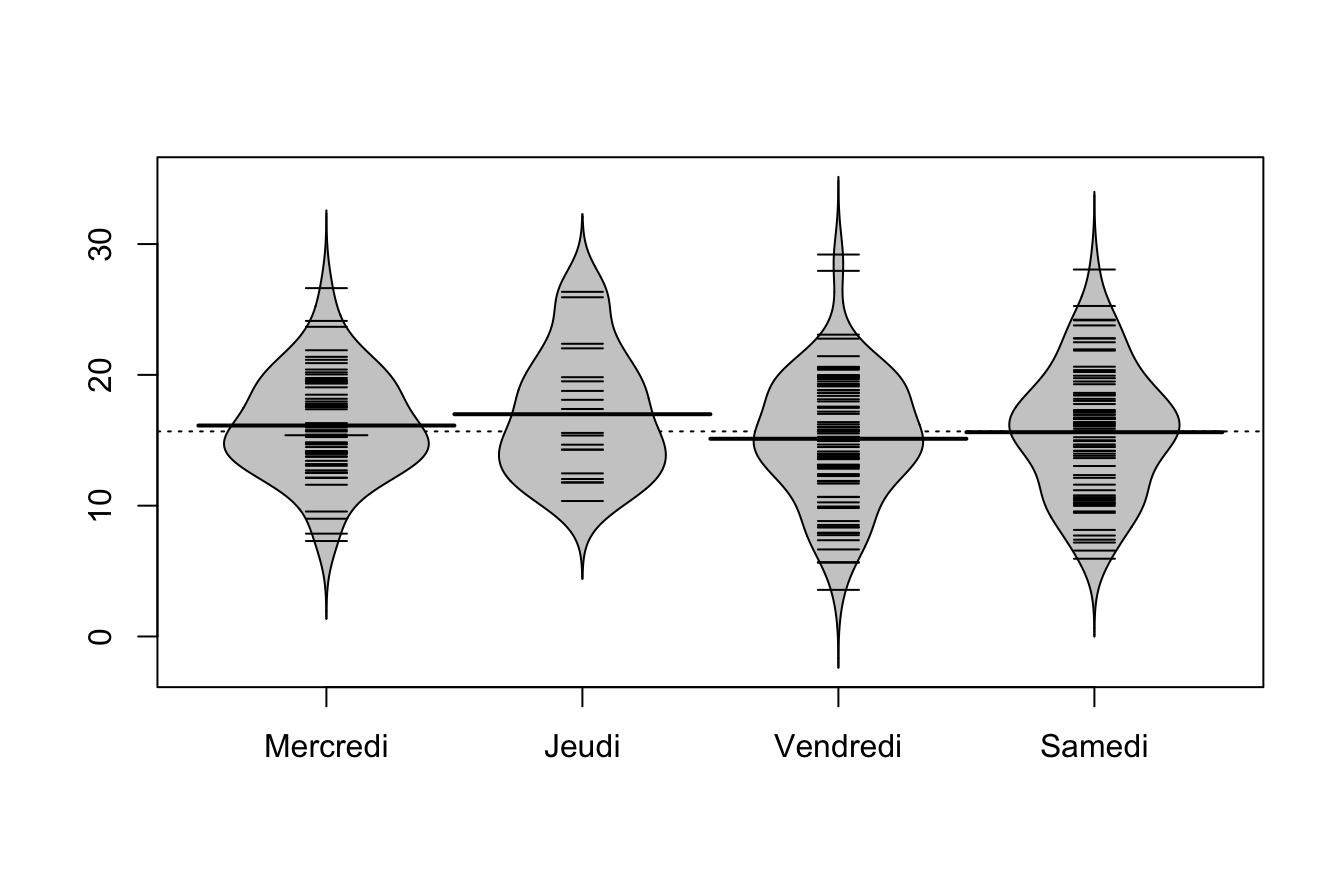

6.4.4 Modélisation simple

La solution la plus simple est d’utiliser la fonction lm() que l’on a déjà vu pour la régression.

monmodel<-lm(don2$PCT~don2$DAY)
summary(monmodel)


Call:
lm(formula = don2$PCT ~ don2$DAY)

Residuals:
     Min       1Q   Median       3Q      Max 
-11.5507  -2.7549  -0.1519   3.2335  14.0845 

Coefficients:
                 Estimate Std. Error t value Pr(>|t|)    
(Intercept)       16.1276     0.5836  27.634   <2e-16 ***
don2$DAYJeudi      0.8637     1.2050   0.717    0.474    
don2$DAYVendredi  -1.0131     0.7656  -1.323    0.187    
don2$DAYSamedi    -0.5097     0.7912  -0.644    0.520    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 4.595 on 237 degrees of freedom
Multiple R-squared:  0.01435,   Adjusted R-squared:  0.001876 
F-statistic:  1.15 on 3 and 237 DF,  p-value: 0.3295

On peut ensuite appliquer une analyse de variance avec anova() sur le modèle pour mesurer la variance totale et la variance résiduelle ainsi que la significativité de la relation.

anova(monmodel)

Analysis of Variance Table

Response: don2$PCT
           Df Sum Sq Mean Sq F value Pr(>F)
don2$DAY    3   72.9  24.293  1.1503 0.3295
Residuals 237 5004.9  21.117

Et on peut effectuer quelques diagnostics sur les résidus :

par(mfrow = c(2,2))
plot(monmodel,c(1,2,3,4))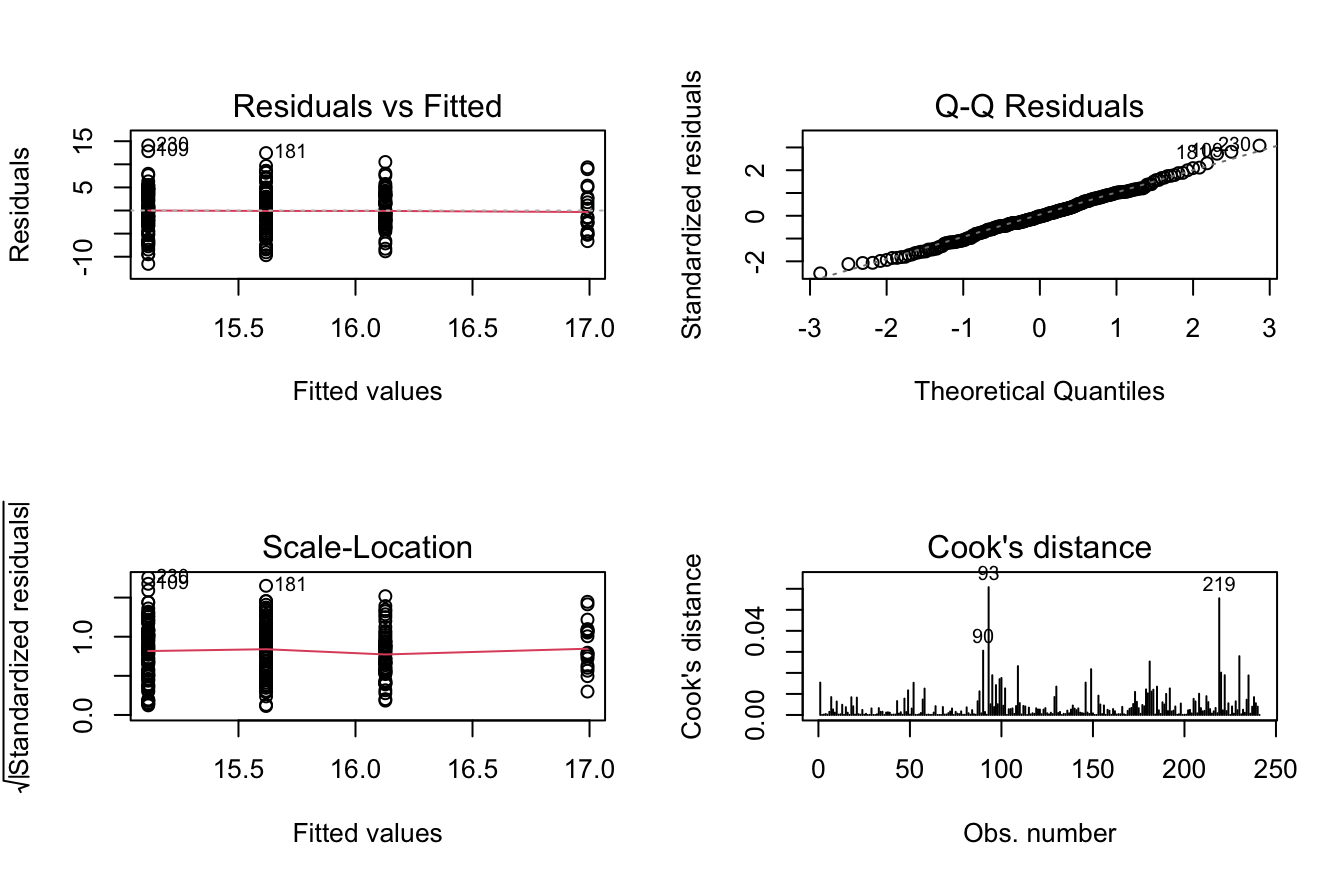

6.4.5 Modélisation avancée

D’un point de vue statistique, l’analyse de variance à un facteur fait appel à des modèles et des hhypothèses plus sophistiqués que le modèle de base présenté ici et comporte de nombreux tests. On se reportera donc ave profit aux trois cours en lignes de Claire Della Vedova pour une approche plus poussée

https://statistique-et-logiciel-r.com/anova-a-un-facteur-partie-1/

https://statistique-et-logiciel-r.com/anova-a-un-facteur-partie-2-la-pratique/

https://statistique-et-logiciel-r.com/anova-a-un-facteur-quand-les-hypotheses-ne-sont-pas-satisfaites/

6.5 Annexe : les variables hybrides

Le nombre de convives (SIZE) n’est ni une variable quantitative continue, ni une variable qualitative de type catégorielle. On peut donc l’appréhender de deux points de vue différents sur le plan statistique

variable quantitative discrète : ce qui permet d’utiliser un modèle de régression linéaire.
variable qualitative ordinale : ce qui permet d’utiliser un modèle d’analyse de variance.

6.5.1 SIZE = quantitative discrète

hist(don$SIZE, breaks=6, col="gray80")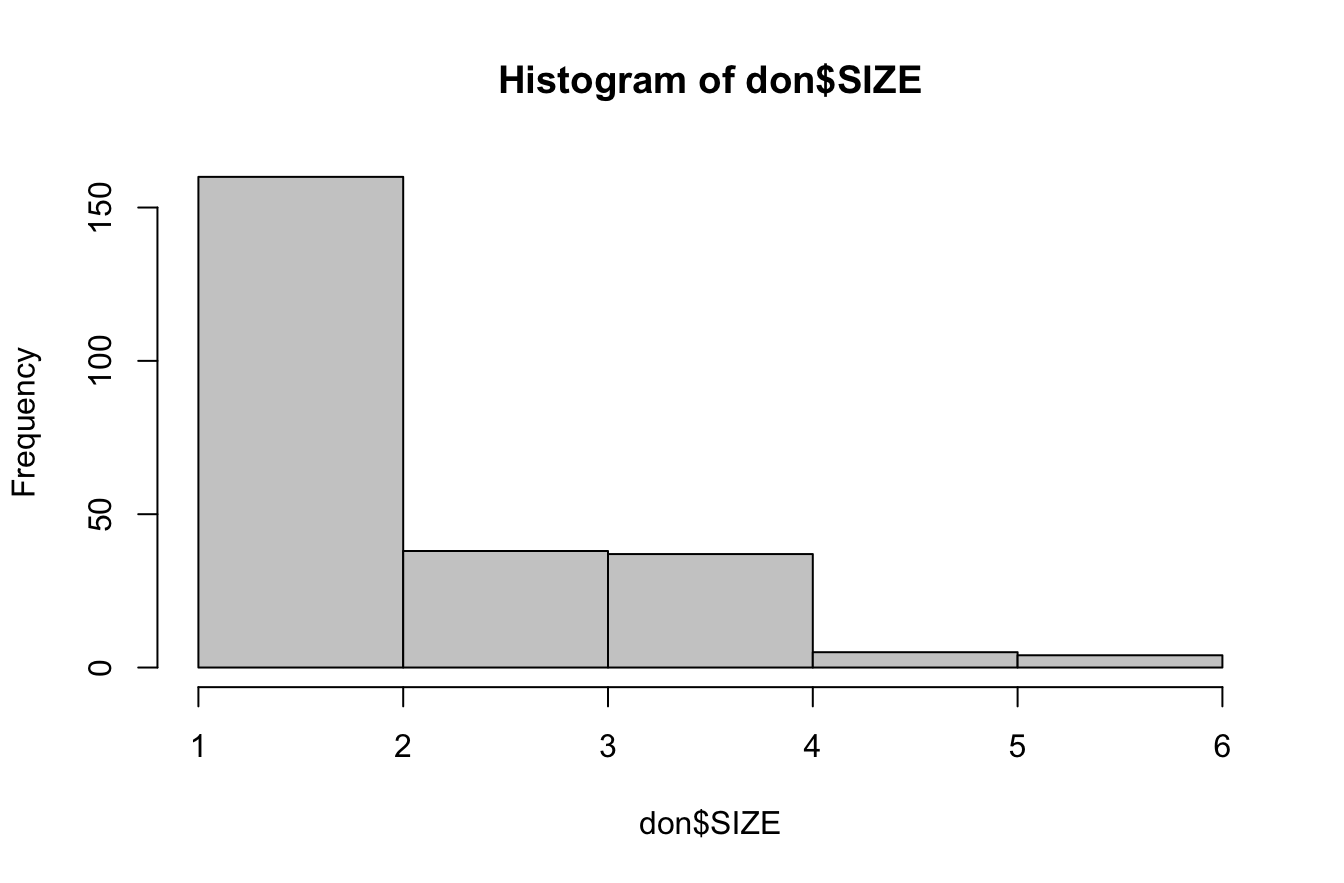

modreg<-lm(don2$PCT~don2$SIZE)
summary(modreg)


Call:
lm(formula = don2$PCT ~ don2$SIZE)

Residuals:
     Min       1Q   Median       3Q      Max 
-12.4591  -2.9738  -0.2625   3.4693  13.2193 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  17.2116     0.8545  20.143   <2e-16 ***
don2$SIZE    -0.5944     0.3108  -1.913    0.057 .  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 4.574 on 239 degrees of freedom
Multiple R-squared:  0.01507,   Adjusted R-squared:  0.01095 
F-statistic: 3.658 on 1 and 239 DF,  p-value: 0.057

plot(don2$SIZE,don2$PCT, col="blue", pch=19, cex=0.7)
abline(modreg, col="red")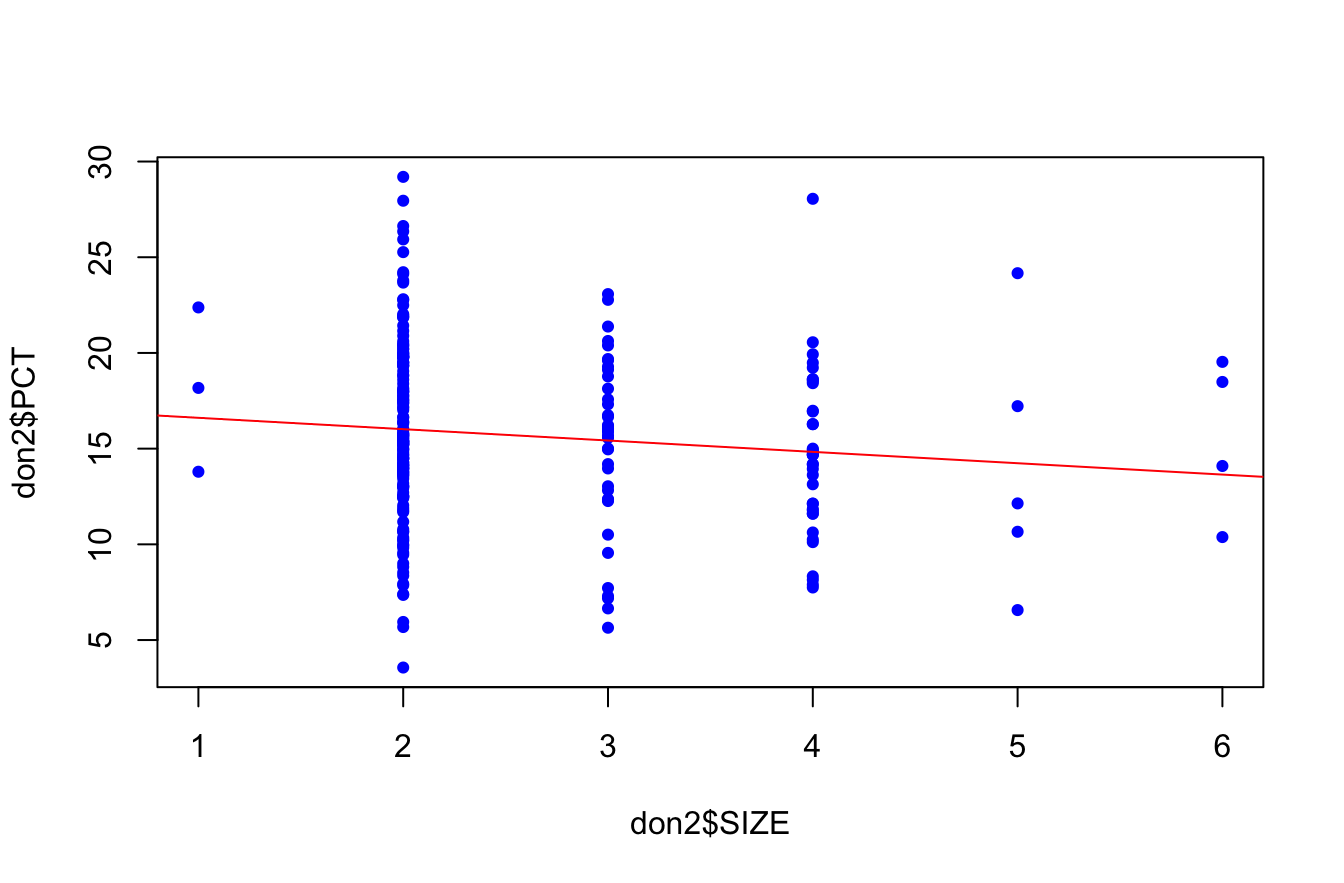

6.5.2 SIZE = qualitative ordinale

On recode les catégories trop rares …

don2$SIZE2<-as.factor(don2$SIZE)
levels(don2$SIZE2)<-c("1-2","1-2","3+","3+","3+","3+")
summary(don2$SIZE2)

1-2  3+ 
157  84

plot(don2$SIZE2)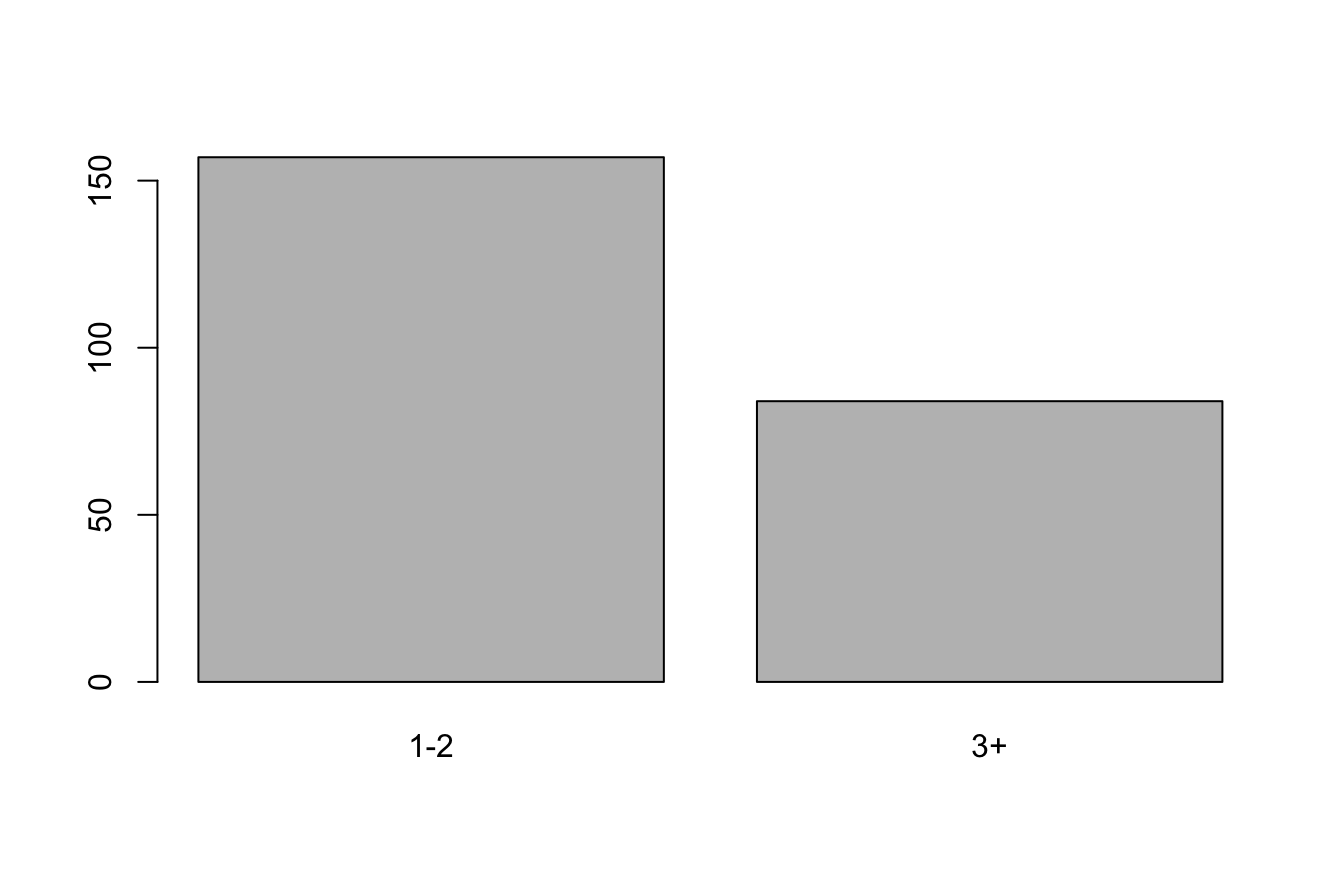

tapply(don2$PCT, don2$SIZE2, mean)

     1-2       3+ 
16.09466 14.89818

tapply(don2$PCT, don2$SIZE2, sd)

     1-2       3+ 
4.626275 4.472961

beanplot(don2$PCT~don2$SIZE2)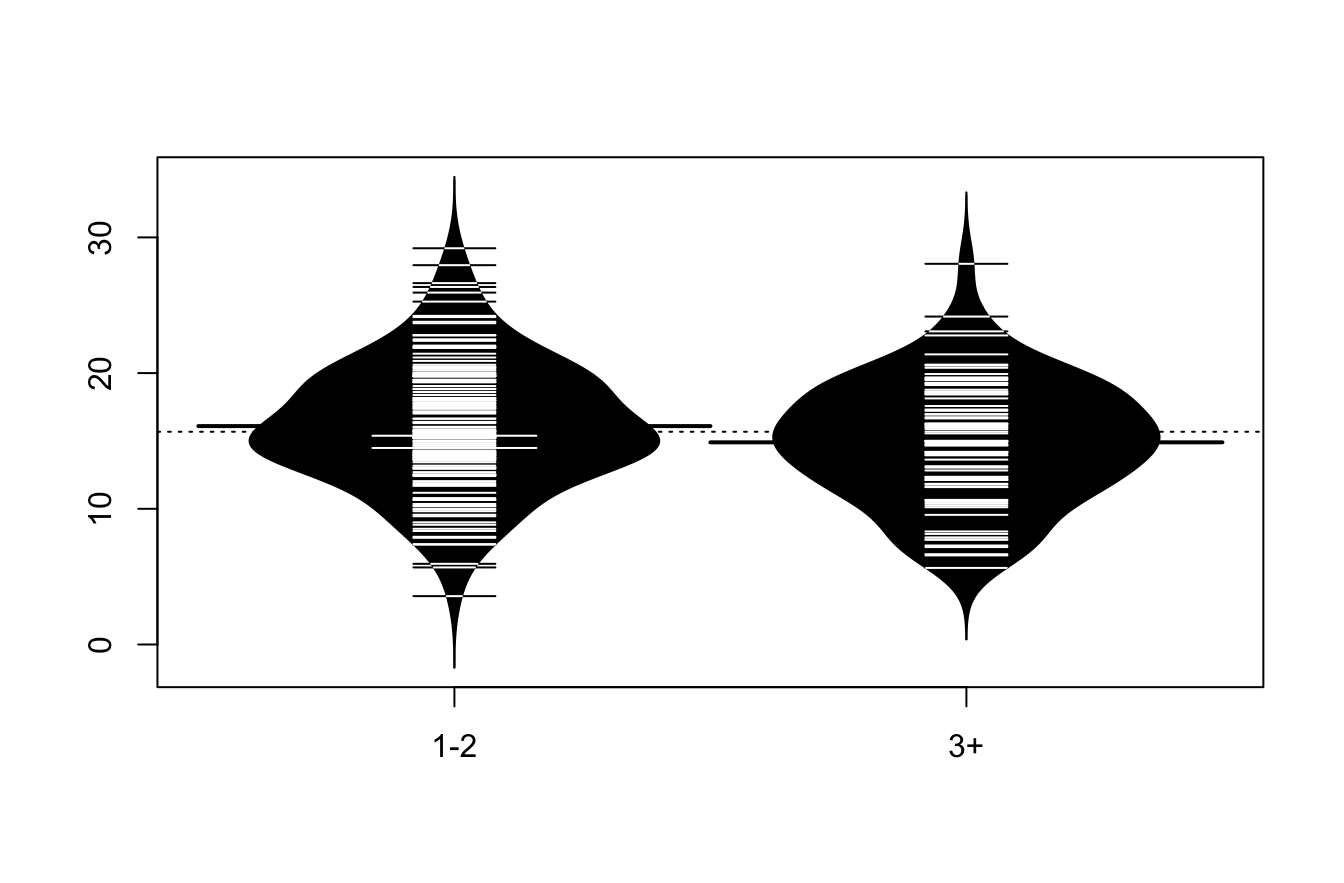

modvar<-lm(don2$PCT~don2$SIZE2)
summary(modvar)


Call:
lm(formula = don2$PCT ~ don2$SIZE2)

Residuals:
     Min       1Q   Median       3Q      Max 
-12.5308  -2.7696  -0.3176   3.4082  13.1553 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)   16.0947     0.3650  44.093   <2e-16 ***
don2$SIZE23+  -1.1965     0.6183  -1.935   0.0541 .  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 4.574 on 239 degrees of freedom
Multiple R-squared:  0.01543,   Adjusted R-squared:  0.01131 
F-statistic: 3.745 on 1 and 239 DF,  p-value: 0.05414